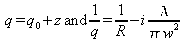Spherical Gaussian wave

We will now introduce here a generalization for the solutions of the Helmoltz equation. The physical signification of those solution will be explain afterwards.

For the solutions of the Helmholtz equation corresponding to paraxial beams along the z-direction, we can write :

where 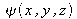 is a complex function representing the difference between a laser beam ansd an homogeneous plane wave.

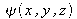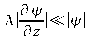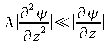If we replace this solution in the Helmholtz equation, with the additionnal hypothesis that the variations of in the z-direction are small over a distance comparable to the wavelength (that is and ), we can write the paraxial wave equation in the following form :

The solution of the paraxial wave equation are well-known. We can thus easily check that the following function (among others) is a solution :

with :

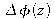• is a complex phase difference.

• q(z) represents a complex radius of curvature, or in other words the transverse variation of the amplitude and the wavefront curvature.

This specific solution, called “fundamental Gaussian mode”, is actually the most important for laser resonators. We will study later this mode more specifically.

By substituting the expression for 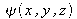in the paraxial wave equation, we obtain that for any (x,y) :

We deduce then that q(z) and 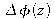must verify :

If we write

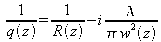
Then

where the “0” indexes correspond to the values for z=0. If we choose the origin so that the curvature radius is infinite (plane wave) at this point, we have 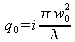. We can then easily show that :

After identification of this relation with we conclude that :

Moreover :

with :

• K/w(z) is a normalization factor

• the first exponential function is the propagation factor

• the second exponential function is a phase difference sometimes called « Guoy » phase shift

• the third exponential function could be broken up in a “spherical wave” factor and a “Gaussian” factor, by replacing q with its expression as a function of R :

where we have used cylindrical coordinates (r²=x² + y²).

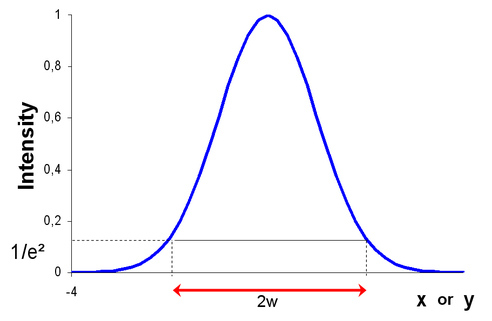
Here we see the Gaussain shape of the transverse profile of the wave for any z position. The intensity profile (proportional to the square of the field amplitude) is then (see figure 10) :

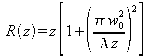• is the radius of curvature of the wavefront at the z abscissa.

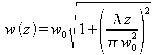• is a measure of the Gaussian decrease of the field amplitude with the distance relative to the z-axis (see figure 10). The parameter w is the distance for which the amplitude is equal to 1/e times (1/e² if we consider the intensity) its value for (x,y) = (0,0)

We also remind the following relations :

• 

• This phase difference means that the phase of the Gaussian wave is shifted by a quantity on the z-axis relatively to a plane wave of the same wavelength that have left the z=0 point at the same moment. The wave undergoes a global phase shift of when passing through z=0.