Fundamentals of Diffraction and Image Formation

Some commonly used functions and their Fourier Transforms

Definition

Table 1 - Definition of a few functions used in this lesson
Table 1 - Definition of a few functions used in this lesson [zoom...]Info

Graphic representation

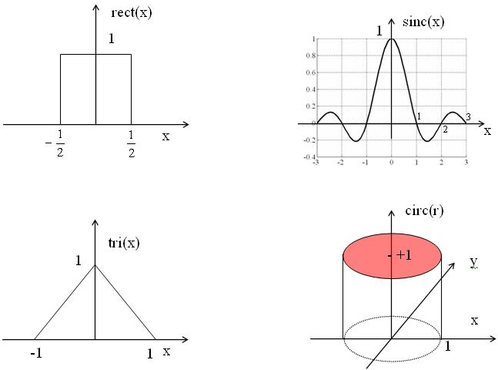
Image I-1 - Graphic representations of a few functions used in this lesson
Image I-1 - Graphic representations of a few functions used in this lesson [zoom...]Info

Fourier transforms of several separable functions in Cartesian coordinates

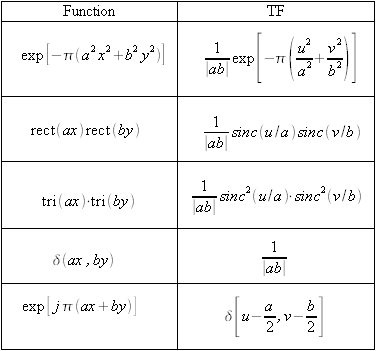
Table 2 - A few functions and their FT
Table 2 - A few functions and their FT [zoom...]Info

The circle function and its Fourier transform

The relation (I-2) for functions of circular symmetry (see paragraph “functions with circular symmetry”) applies, with:

I-3 Info

By replacing (I-3) in (I-2), we obtain:

I-4 Info

We note: 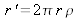; the integral bounds in relation (I-4) are equal to 0 and .

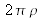Therefore:

Using the relation:

where J1(x) is defined as the Bessel function of first order, we finally obtain:

This function is represented on figure I-2.

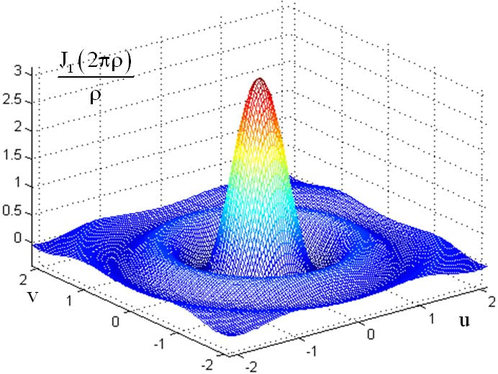
Image I-2 - Fourier transform of the circle function
Image I-2 - Fourier transform of the circle function [zoom...]Info

We note that the Fourier Transform of the function circle has a circular symmetry. It is composed of a central peak and a series of concentric rings of decreasing amplitudes.

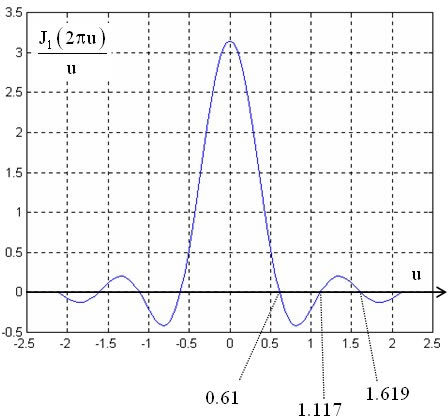
Image I-3 - Radial profile of the function represented on figure I-2.
Image I-3 - Radial profile of the function represented on figure I-2. [zoom...]Info

Figure I-3 represents a radial profile of this function. The zeros are not regularly spaced along each ray as it is the case for the sinc (cardinal sine) function. The radius of the central peak is equal to 0.61.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Separable functionsScalar theory of diffraction