
Image formation under monochromatic illumination
We consider an object located at a distance do in front of the lens; at a distance di (in the image plane) we have a field distribution Ui (xi,yi) (see figure IV-9).
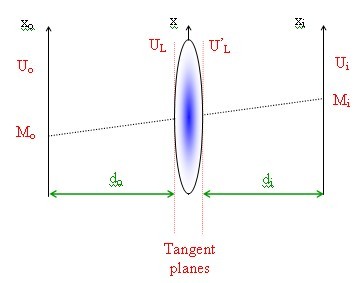
We define the magnification Gs =di /do .We assume that :
(the Gaussian lens formula is satisfied).
We first consider the image predicted by geometric optics. It is simply a reversed and dilated version of the object:
On the wave optics point of view, and taking into account the linear property of the propagation phenomenon, the expression of Ui is a superposition integral (Huygens-Fresnel principle):
where h(Mi,Mo) is the amplitude of the field produced at the point Mi(xi,yi) by a point source of unit amplitude and located at the point Mo (xo,yo) in the object plane.
h(Mi,Mo) fully characterizes the optical properties of the system. It is called the point-spread function of the imaging system.
To determine h, we consider a point source in the object plane δ(Mo) (see figure IV-10).
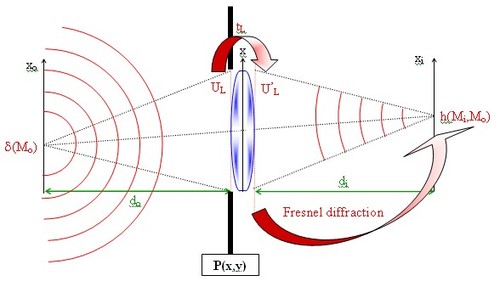
This point source emits a spherical wavelet which propagates on a distance do until the plane tangent to the lens. At this plane, the field amplitude is:
This field meets the pupil function P(x,y) characterizing the finite dimensions of the lens. We apply the phase transform:
to this field to obtain the transmitted field U'L. Using Fresnel diffraction law on a finite distance di gives the expression of the point-spread function:
h(Mi,Mo) represents the Fraunhofer diffracting figure of the lens aperture (the pupil) centered at point xi =-Gsxo ; yi =-Gsyo .
Relation between object and image
We define
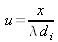 ;
;
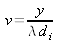 and x'o
=-Gsxo
; y'o=-Gsyo. the expression (IV-9) becomes:
and x'o
=-Gsxo
; y'o=-Gsyo. the expression (IV-9) becomes:
We deduce that the point-spread function is spatially invariant, i.e.:
Defining
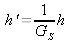 , the superposition integral (IV-8) becomes:
, the superposition integral (IV-8) becomes:
The image appears as the convolution of the point-spread function with the image obtained with geometric optics.
This result shows that when we take into account the effect of diffraction, the image is no longer the exact replica of the object. It is attenuated by the convolution with the system point spread function, which affects mostly the fine details in the object.