Superposition of two spherical waves

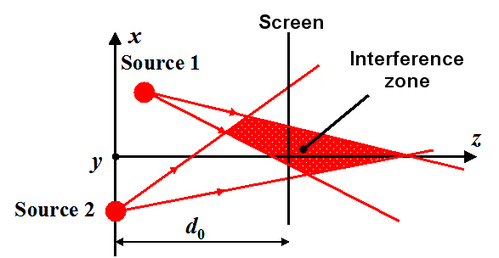
Let us consider two co-polarized (polarized along x direction) spherical waves propagating towards z positives. Figure 5 illustrates this scenario.

In this case, we simply have:

for the first wave, and:

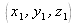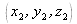for the second one. Note that and are the coordinates of the point sources. For all coordinates 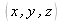we have:

The interference phase is , i.e:

Figure 6 shows the interference field in the superposition zone of the two waves on the (x, z) plane to the left, and on the cross-section to the right (plane (x, y, z = d0)).

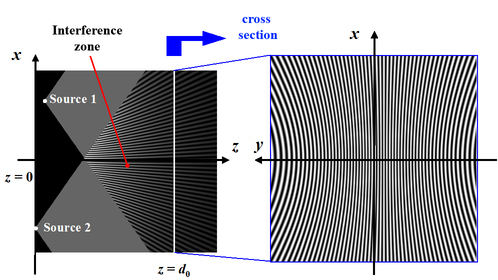
We can see that the amplitude of interferences decreases with distance from the sources, due to the factor 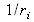of each term of the complex amplitude.

In space (x, y, z), a bright fringe is localized by the condition:

i.e:

with . This relation is not simple to use.

However, we can write the interfringe distance explicitly in the case of a parabolic approximation. Suppose that 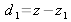and . Assuming this condition is true, a bright fringe is localized by the condition:

which gives:

with:

Let us consider an ideal case: suppose that the sources are localized symmetrically on the x axis, one at 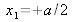and the other at with 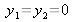and 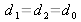and that the plane observation is defined as 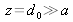. Figure 7 illustrates this geometry.

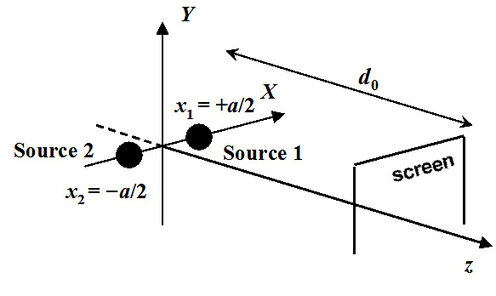
In this case it simply follows that:

With this configuration, the fringes are rectilinear and vertical, parallel to the y axis. We can see in figure 6 that this result corresponds to the center of the screen. The bright fringe of the order k is thus localized at xk such that:

And the next bright fringe of the order k+1 is localized at xk+1 such that:

The interfringe distance is thus:

With the parabolic approximation, the interfringe distance is a constant according to the direction x.