
Reconstructing the object field
Principle of reconstruction by transmission
The reconstruction of the object field encoded within the hologram is based on the principle of light diffraction. If the holographic plate is illuminated after its development using the same reference wave used in the recording process, the light will diffract into three orders of diffraction if the diffraction network is sinusoidal. The complex amplitude which is transmitted is as follows :
Respective to the three terms in this equation, the three orders of diffraction are : the 0-order, the +1-order and the -1-order.
-
The -1-order is also called the real image; it is directly proportional to the conjugate complex of the object wave. This image is pseudoscopic, taking in to account its inverted contours (phase conjugation/retroflection) ;
-
The 0-order is proportional to the sum of the squares of the modules of the two waves ;
-
The +1-order is the most adapted to observation given that it is directly proportional to the original complex field. This order gives a virtual image and is characteristically orthoscopic.
During reconstruction using the “in line” configuration the three orders are superimposed and the virtual image is thus mixed with the real image and the direct transmission of the reference beam.
Figure 8 depicts the principle of reconstructing a hologram by “off axis” transmission. This configuration has the advantage of not causing the three orders to be superimposed during the reconstruction process, contrary to the “in line” configuration. The “off axis” system was used for the first time by Leith and Upatnieks [ , ] following the invention of the first lasers.
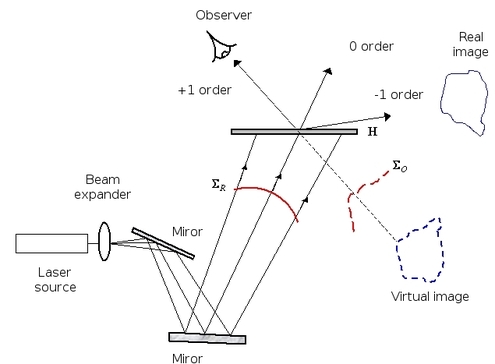
The way that a hologram is reconstructed makes it the reference wave which serves as the key for the decrypting of the encoded information. Indeed, the recording wave has a phase and amplitude distribution which is unique to that particular wave and this distribution is the key to the decoding.
It is possible to observe the real image by illuminating the plate with the complex conjugated component of the reference beam (figure 9).

The principle of reconstruction by reflection
After the hologram has been recorded by the configuration shown in figure 6, the reconstruction is carried out according to the same principle which we have seen in transmission holography. Indeed, the hologram is illuminated by a beam which is identical to the reference beam, the latter is refracted by the holographic plate and the observer sees the image forming at the back of the plate. The image can be virtual or real.
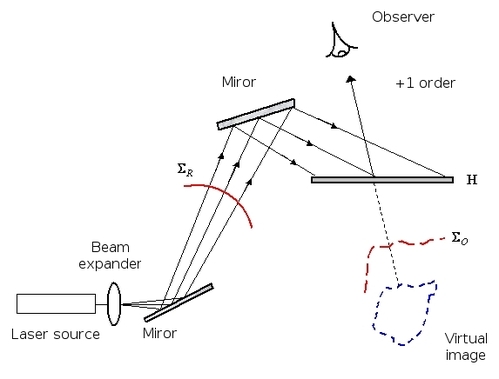
Formation of the image in the +1-order
The formation of the image in this process of recording and reconstruction can be explained using the diffraction formula.
Let's consider that the observer is looking at the object reconstructed in the +1-order which conforms to the initial object. Let's also consider that the encoded hologram on the photosensitive plate is spatially limited by the physical size of the recording plate.
Note that
 is the function designating “the size of the photosensitive plate” :
is the function designating “the size of the photosensitive plate” :
Where
 and
and
 are the width and the height of the plate.
are the width and the height of the plate.
The diffracted field in the +1-order, that is to say at the distance
 from the plate, is expressed by Fresnel diffraction integral :
from the plate, is expressed by Fresnel diffraction integral :
Since the object field
 can also be expressed by a Fresnel transform we get :
can also be expressed by a Fresnel transform we get :
With
And
Taking into account the properties of Fourier transforms, we finally get :
With the enlargement function :
The reconstructed object in the +1-order is therefore proportional to the initial object field: it has the same amplitude and phase and thus the same contours and it is proportional to the exposure time and the transmittance gradient of the plate in the linear zone. Also, the reconstructed object is convoluted by an enlargement function
 which is proportionnal to the size of the recording plate. The convolution function is a two dimensional sinc function. According to Rayleigh's criterion, this function has a width and height equal to :
which is proportionnal to the size of the recording plate. The convolution function is a two dimensional sinc function. According to Rayleigh's criterion, this function has a width and height equal to :
A nimerical application with the values
 ,
,
 for a silver photo plate of
for a silver photo plate of
 gives
gives
 and
and
 .
.
These quantities determine the resolution in the image plane of the +1-order.
The spatial resolution is thus proportional to the recording distance and inversely proportional to the width of the recording plate. In order to increase the resolution, the object must be placed nearer to the photo plate, using the largest possible photo plate.