Choosing a coverage factor

If the measurement results are distributed according to a normal law around the average value m (cf. figure 1), table 3 shows the respective values of the coverage factor k and the confidence level 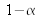sont rassemblées dans le tableau 3.

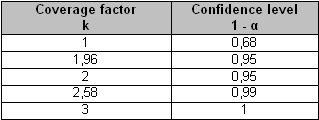
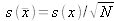These values are only strictly valid when the number N of replications of measurements is high (typically N≥30). This is rarely the case in practice, and we must therefore use Student's t-distribution followed by the variable is the arithmetic mean of N independent observations xk ofx and is the experimental standard deviation of the average . Note that Student's t-distribution is only valid if the random variable x follows a normal law of mathematical expectation µx and of standard deviation .

As a consequence, if the measurand Y is a single quantity X following a normal law, such as Y=X and if X is estimated by the arithmetic mean 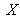of N independent replicate observations Xk of X, with an experimental standard deviation of the average , then is distributed according to Student's t-distribution with

that is to say

or

In these expressions, 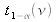is the value of t for a given value of the parameter ν (number of degrees of freedom) such as the interval is associated with a confidence level 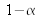. In other words, the expanded uncertainty is