Uncertainty on the reference

Using the propagation of uncertainties law, express the relative standard uncertainty u(E)/E in function of u(IL)/IL and u(D)/D.

The model for the measurement is 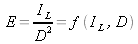. It is a product-quotient model, hence:

In order to determine the relative standard uncertainty u(IL)/IL or the luminous intensity emitted by the standard lamp, we consider the information provided by its calibration certificate.

The standard lamp is calibrated with an expanded relative uncertainty of 1% (k=2). Deduce the value of the associated relative standard uncertainty u 1 (IL )/IL .

With a coverage factor (k=2), we have:

The standard lamp shows a total range drift of 0.3% between two successive calibrations. Applying a uniform probability law, calculate the relative standard uncertainty u 2 (IL)/IL associated with this drift.

In the absence of any additional information, we consider that the time drift is associated with a uniform probability for the time intervals between 2 successive calibrations. We thus have:

The variation of the luminous intensity IL with the supply current i does not follow a linear law. We have:

The ammeter used to measure the current going through the lamp is calibrated with a 0.05% expanded relative uncertainty (k=2). Deduce the value of the associated relative standard uncertainty u3(I L )/IL.

For 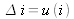standard uncertainty on the current "i", we have 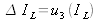hence :

standard uncertainty on the current hence :

From the previously obtained results, deduce the value of the relative combined standard uncertainty u(IL)/IL.

that is to say

The measurement of distance D s 3m with an estimated variation interval of ±5mm. Deduce the value of the relative uncertainty u( D )/D .

From the previous calculations, give the value of the standard uncertainty uréf(E) for a reference illumination of 100 lux.

with 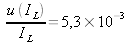and hence

That is to say for E=100 lux, uréf(E)=0,53 lux.