Loi ABCD appliquée aux faisceaux gaussiens

Un mode de cavité stable est caractérisé par le fait que le faisceau garde la même structure transverse et la même phase (modulo 2 pi) après un aller-retour dans la cavité (ou après un tour pour une cavité en anneau).

Plus précisément, le rayon de courbure complexe q(M) doit être conservé quelque soit le point M considéré. Autrement dit, si est la matrice de transfert à partir du point M (attention, T(M) est différente en fonction du point M choisi), on doit avoir par application de la loi ABCD (voir paragraphe sur "les matrices de transfert et loi ABCD") et quelque soit M :

C'est une condition complètement générale qui s'applique à toute cavité résonante. En identifiant les parties réelles et imaginaires de cette relation, on obtient deux équations qui définissent respectivement la géométrie du système (en particulier la position des waists) et les fréquences de résonance de la cavité.

La condition de stabilité découle également de la loi ABCD ci-dessus. On peut en effet la réécrire :

ou encore

soit

qui vaut aussi

Pour que le faisceau existe, il faut que w soit fini, ou encore que (D-A)²+4BC soit strictement négatif (afin que la partie imaginaire de 1/q soit non nulle).

Comme la matrice T est unitaire, on a AD-BC = 1 et la condition se réécrit donc :

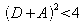ou encore 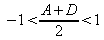soit

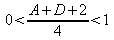
On retrouve la condition de stabilité démontrée précédemment dans le cadre de l'optique géométrique, mais ici on remarque que l'inégalité est stricte : on exclut donc les cas limites où qui représentent des cavités instables pour les faisceaux gaussiens.

La loi ABCD donne également les caractéristiques du faisceau gaussien au point M :

et

On choisit souvent M à un waist du faisceau, c'est à dire à un endroit où le rayon de courbure R est infini. On constate alors que A=D dans la matrice T (M). Inversement, si A=D alors le point M est à un waist de la cavité.