Solutions harmoniques des équations de propagation

Les solutions de l'équation de propagation sont des fonctions scalaires ou vectorielles. Elles doivent reproduire « à un instant ultérieur » la même fonction « plus loin ». Pour être solution de l'équation, la fonction sera une fonction du type : .

Généralement, pour les ondes se propageant vers les positifs on s'intéresse aux solutions harmoniques qui s'écrivent :

où est le vecteur d'onde :

et représente le vecteur orthonormé décrivant la direction de propagation de l'onde, est la longueur d'onde dans le vide et la longueur d'onde dans le milieu. Pour les ondes se propageant vers les négatifs on s'intéresse aux solutions harmoniques qui s'écrivent :

Dans le cas où l'onde est plane et monochromatique, la propagation est rectiligne, suivant z par exemple, dans le vide l'équation de propagation s'écrit simplement :

et la solution se propageant vers les z positifs est :

La surface d'onde associée à la propagation est donnée par des plans équiphases tels que :

elle est perpendiculaire au vecteur d'onde .

Dans le cas où l'onde est sphérique, la propagation est à symétrie sphérique et la solution se propageant vers les positifs est :

Dans ce cas, la composante du champ ne dépend que de r avec un système de coordonnées centré sur le point de convergence (ou de divergence). Il s'agit du point source si c'est une onde divergente. d'un point de focalisation si c'est une onde convergente.

La surface équiphase qui décrit la surface d'onde est une sphère centrée sur le point source. Une onde divergente s'écrit :

Pour une onde convergente :

Il est utile d'expliciter le formalisme dans le cas d'un système de cordonnées rectangulaires (cartésien). Sur la figure 1, la source est située au point de cordonnées et l'onde se propage suivant les z positifs.

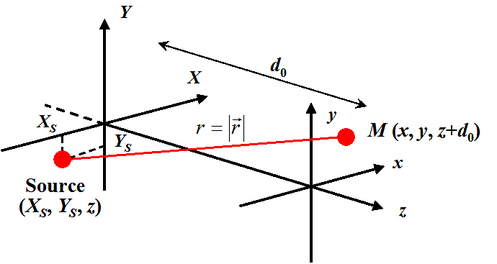
D'après la figure, on constate que :

Le front d'onde propagé dans le plan situé à la distance de la source s'écrit [1] :

Cette expression ne se manipule pas facilement. Afin de réduire la complexité de l'écriture en coordonnées cartésiennes, on introduit des approximations sur la distance entre la source et le front d'onde observé. Les approximations sont basées sur un développement de la racine carrée présente dans la fonction exponentielle [1]. En effet, dans le cas où , nous avons :

et en ne retenant que les deux premiers termes du développement limité, il vient :

Au dénominateur, on retient une approximation au premier ordre, soit :

Ainsi, le front d'onde propagé dans le plan situé à la distance de la source s'écrit désormais :

La validité de cette approximation est déterminée par les erreurs induites lorsque les termes d'ordres supérieurs du développement ne peuvent plus être négligés. Une condition suffisante est que la variation maximale de phase induite par le terme en a2/8 génère une variation de phase qui soit très inférieure à 1 radian. Le lecteur pourra vérifier que la condition de validité est la suivante [1] :

Pour fixer les ordres de grandeur, considérons une source située en et une région d'observation carrée de 50 mm de coté, la longueur d'onde de la source étant égale à 0,5 μm, on détermine .