Optical resonators and Gaussian beams

Physical properties of Gaussian beams

The main basic expressions related to Gaussian beams were mathematically obtained in the previous paragraph. We will now describe their physical signification.

Let's take again the origin at the waist position w0, corresponding to a plane wave (infinite radius of curvature). We have defined the Rayleigh length : .

We also wrote the equation describing the evolution of w versus z :

w(z) is an hyperbola (we could also write the previous relation : ).

Main useful parameters

Let us remind the main parameters and results previously described :

  • w(z) is the dimension of the laser spot (the “radius” if the spot is circular) in the plane perpendicular to the propagation, at a distance z from the origin. Precisely, it is the radius (at 1/e for the amplitude, or 1/e² for the intensity) of the transverse Gaussian profile at the z abscissa.

  • When z increases, the beam expands in the transverse direction while its amplitude on the z-axis decrease (energy conservation). The profile shape remains Gaussian.

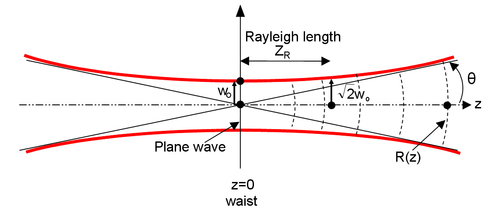
  • The size of the beam at the origin, w0, is minimal : the beam will diverge from this point (see figure 11). This minimal dimension is called “beam waist” (the waist is the radius of the spot. The diameter is of course given by 2 w0).

  • At the waist, the wavefront is a plane.

Figure 11 : Properties of a Gaussian beam
Figure 11 : Properties of a Gaussian beam [zoom...]Info

  • The beam divergence is given by the limit of w/z when z goes to infinity : or for a small divergence

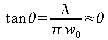
  • The Gaussian characteristics of the beam are essentially important in the vicinity of the beam waist. Indeed, when z increases, the complex radius of curvature becomes close to R and the wave could be considered spherical.

  • The Rayleigh length is the distance (from the waist) where the beam area is twice the beam area at the waist (the radius is 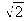times bigger). This parameter is useful to define a “collimated” beam : over this length, the beam size is nearly constant (between and ) - see figure 11.

Order of magnitude :

For a tightly focused laser beam (w0 = 10 µ) and a 1 µm wavelength, we find ZR = 314 µm and a divergence (half-angle) of 1,8 degrees.

If we consider a “big” waist (1 mm), we find ZR = 3,14 m and a divergence (half-angle) of 0,018 degrees. We then obtain a so-called “collimated beam”.

The divergence of a Gaussian beam is inversely proportional to the size of its waist. In the framework of Gaussian optics, “collimating a beam” is the same thing as “having a big waist”.

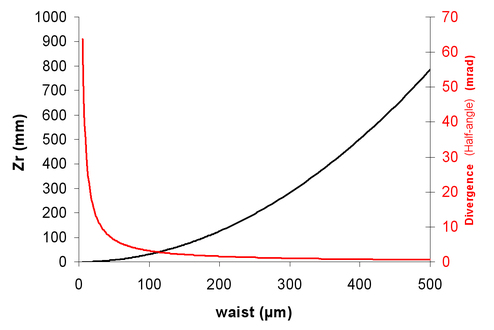
We observe on figure 12 the evolution versus z of the Rayleigh length and of the divergence for a 1 µm

Figure 12 : evolution of the Rayleigh length and of the divergence versus z, for a 1 µm wavelength
Figure 12 : evolution of the Rayleigh length and of the divergence versus z, for a 1 µm wavelength [zoom...]Info

Other useful relations

Some very practical relations could be deduced from the previous ones, as for example :

and

Those relations are used to find the waist size and its position starting for experimental measurements of R and w.

AccueilOutils transversesNouvelle pageInformations sur le cours (ouvrir dans une nouvelle fenêtre)Spherical Gaussian waveGaussian beams focusing and mode matching