ABCD law and Gaussian beams

For a stable cavity mode, the transverse structure of the beam as well as its phase (modulo 2 pi) remains the same after a round trip in the resonator.

More precisely, the complex radius of curvature q(M) has to be conserved whatever the M point may be. In other words, if 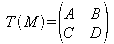is the transfer matrix with M chosen as the origin (be careful, T(M) is different for each M !), we must have for every M (ABCD law) :

This is a general condition that could be applied to every resonator.

If we identify the real and imaginary parts of this relation, we obtain two equations that define the geometry of the system (particularly the waist(s) position) and the resonant frequency of the cavity respectively.

The stability condition is also a consequence of the ABCD law. We could actually write :

or

thus

but 1/q is also equal to

The beam could only exist if w is finite. The imaginary part of 1/q should consequently be different from zero, which means that (D-A)²+4BC has to be strictly negative.

The T matrix being unitary, we have AD-BC = 1 and the condition could be written :

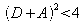that is 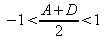or

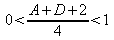
We find again the stability condition previously demonstrated in the framework of ray optics, but here it is important to notice that the inequality is a strict one : the limits are excuded, which means that the cases where 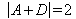are unstable resonators for Gaussian beams.

The ABCD law also defines the Gaussian beam characteristics in M :

and

M is often positioned at a cavity waist (R = infinity). We then have A=D in T(M). Inversly, if we find A=D then it means that M was located at a cavity waist.