
Propriétés des lentilles relatives à la transformation de Fourier
Introduction
Dans ce qui suit on supposera que l'éclairage est monochromatique et on s'intéresse à la distribution d'amplitude de la lumière dans le plan focal image de la lentille. Trois cas seront envisagés selon la position de l'objet par rapport à la lentille.
Objet placé contre la lentille
Soit un objet plan de transmittance en amplitude to(x,y) placé immédiatement en avant d'une lentille convergente (voir figure IV-4).
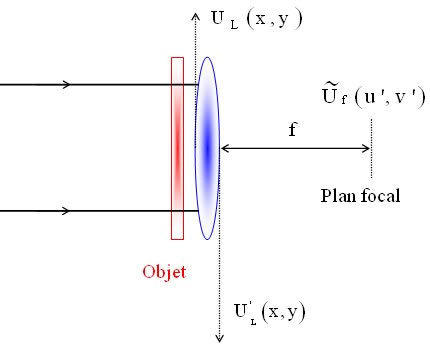
On suppose que l'objet est uniformément éclairé par une onde plane d'amplitude A tombant sous l'incidence normale. Dans le plan tangent à l'entrée de la lentille on peut écrire :
La distribution du champ immédiatement à l'arrière de la lentille devient alors :
Où pour tenir compte de la dimension finie de la lentille, on définit la fonction pupillaire :
Afin de déterminer la distribution du champ dans le plan focal, appliquons la formule de diffraction de Fresnel pour z=f (Eq. III-2) :
En laissant de côté le facteur de phase constant exp(jkf) et en remplaçant U'L(x,y) par sa valeur, on constate que les facteurs quadratiques de phase à l'intérieur de l'intégrale se compensent :
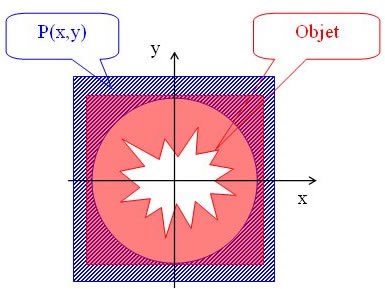
Si les dimensions spatiales de l'objet sont inférieures à l'ouverture de la lentille (voir figure IV-5), le facteur P(x,y) n'intervient plus car le champ à l'endroit où l'objet est opaque est nul et U L (x,y) P(x,y)=UL (x,y) :
-
On voit que l'amplitude complexe dans le plan focal est la figure de diffraction de Fraunhofer du champ incident devant la lentille bien que la distance d'observation soit égale à la distance f qui peut être très inférieure aux distances usuelles d'observation définies dans le chapitre 3.
-
Mis à part les facteurs multiplicatifs devant l'intégrale, l'expression précédente (IV-3) est donc simplement une transformation de Fourier :
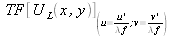
-
Le terme de phase quadratique devant la TF exprime ce que l'on appelle une «courbure de phase».
-
Généralement, on s'intéresse à If la distribution de l'intensité, appelé «spectre angulaire de puissance» ou «énergie spectrale» de l'objet :
Objet placé avant la lentille
Considérons l'objet (caractérisé par sa transmittance en amplitude t0 (x,y) situé à la distance d devant la lentille (voir la figure IV-6).
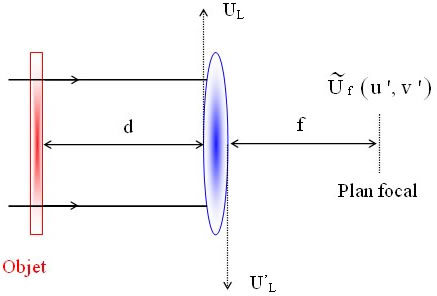
C'est un montage plus général que le précédent (défini pour d=0). On suppose que l'objet est uniformément éclairé par une onde plane d'amplitude A tombant sous l'incidence normale.
Soit
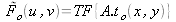 et
et
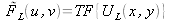 . On sait que la fonction de transfert du phénomène de propagation permet de calculer
. On sait que la fonction de transfert du phénomène de propagation permet de calculer
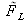 à partir de
à partir de
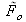 (Eq. II-12 partie :Théorie scalaire de la diffraction) :
(Eq. II-12 partie :Théorie scalaire de la diffraction) :
La lentille sera considérée dans l'approximation paraxiale donc les rayons sont très peu inclinés par rapport à l'axe optique :
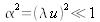
et
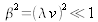 Un développement limité de la racine dans l'expression précédente implique
Un développement limité de la racine dans l'expression précédente implique
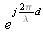 est un terme de phase constant que l'on peut omettre dans ce qui suit. Par ailleurs, on connait la propagation de UL
(x,y) qui est contre la lentille jusqu'au plan focal. Elle est décrite dans le paragraphe précédent (Eq. IV-3):
est un terme de phase constant que l'on peut omettre dans ce qui suit. Par ailleurs, on connait la propagation de UL
(x,y) qui est contre la lentille jusqu'au plan focal. Elle est décrite dans le paragraphe précédent (Eq. IV-3):
Or en appliquant la fonction de transfert de propagation (Eq. IV-4), il vient :
dans l'argument de l'exponentielle on met en facteur 1/(λf)² et après avoir simplifié par λ, on multiplie par 2/2 pour faire apparaître
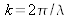 :
:
Donc l'expression (IV-5) devient :
En regroupant les exponentielles et en mettant en facteur
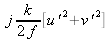 on trouve :
on trouve :
ou encore :
Remarquons qu'un facteur de phase précède la TF de l'objet. Ce facteur s'annule pour d=f (si l'objet est placé dans le plan focal objet de la lentille). Dans ce cas la courbure quadratique de phase disparaît pour donner lieu à une transformation de Fourier exacte.
Objet placé après la lentille
On considère les mêmes conditions d'éclairement que précédemment : onde plane monochromatique d'amplitude A et à incidence normale. L'objet reçoit une onde sphérique qui converge vers le foyer image de la lentille (voir figure IV-7).
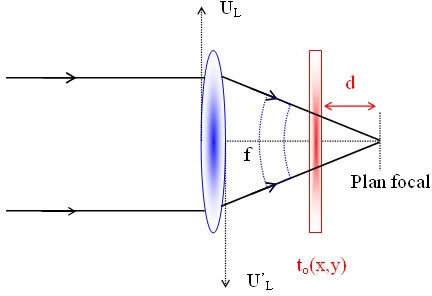
En se basant sur la figure IV-8,
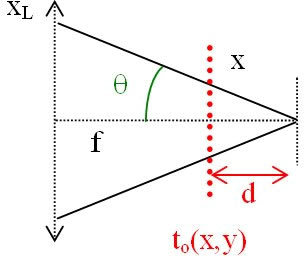
Un calcul simple dans le cadre de l'optique géométrique avec l'approximation paraxiale montre que :
-
l'amplitude au niveau de l'objet est
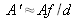 .
.
-
l'étendue finie de la zone éclairée, intersection du plan objet et du cône de lumière peut être représentée par la fonction pupillaire effective : P(xL,yL)=P(xf/d,yf/d).
-
l'onde sphérique qui éclaire l'objet peut être écrite :
Dans ces conditions, l'amplitude complexe Uo(x,y) du champ transmis par l'objet s'écrit :
En appliquant la diffraction de Fresnel (Eq. III-2) pour passer du plan objet au plan focal (z=d), l'amplitude dans ce dernier plan s'écrit :
En remplaçant Uo(x,y) (Eq. IV-7) par sa valeur, on s'aperçoit que le terme de phase quadratique à l'intérieur de l'intégrale s'annule.
Mis à part le terme de phase quadratique, la distribution de l'amplitude dans le plan focal est donc la TF de la portion de l'objet limitée par la projection de l'ouverture de la lentille dans le plan de cet objet. Ce résultat est le même que celui déjà obtenu quand l'objet est placé tout contre la lentille. Cependant, ici, l'expérimentateur peut modifier l'échelle de la TF.
En augmentant d, on augmente les dimensions de la TF jusqu'à ce que l'objet vienne contre la lentille (d=f)
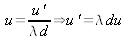 . Cette propriété peut être utile dans les applications sur le filtrage spatial.
. Cette propriété peut être utile dans les applications sur le filtrage spatial.