Démodulation par transformée de Fourier

Cette méthode, apparue en 1982 [ ], avait été utilisée dans un premier temps à une dimension avec les algorithmes FFT unidimensionnels, puis elle a évolué vers sa forme bidimensionnelle globale avec l'apparition des algorithmes FFT2 rapides. Dans les deux cas, après transformée de Fourier de la figure de franges, on obtient un spectre tri-modal symétrique par rapport à l'origine.

La méthode présente le gros avantage de réduire considérablement le niveau de bruit de la carte de phase démodulée mais dégrade la résolution spatiale. La modulation de phase est purement spatiale [ ] :

On peut évidemment envisager le cas u0 =0 ou le cas v0 =0, le principe de la méthode reste valable. Dans la suite on considérera ce dernier cas.

Le choix de la fréquence porteuse doit tenir compte du nombre de pixels de la caméra et des périodes d'échantillonnage en vertical et en horizontal sur la matrice CCD. Si on note px et py les tailles des pixels sur la CCD, alors les fréquences d'échantillonnage sont 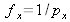et . Dans la pratique, il faudrait également tenir compte de la Fonction de Transfert de Modulation (FTM) de l'optique d'imagerie associée à la matrice CCD.

La fréquence porteuse doit respecter le théorème de Shannon : u0 <ƒx/2 et v0 <ƒy/2. Dans le plan de Fourier de l'interférogramme, l'écart fréquentiel entre deux valeurs spectrales est de ƒx /N en horizontal et ƒy/M en vertical où N et M correspondent au nombre de pixels de la matrice image (sans zéro-padding de l'interférogramme).

Si on souhaite avoir une porteuse spatiale centrée sur ƒx/4 (resp. ƒy/4), c'est à dire au milieu de la fenêtre de fréquences positives, alors la période spatiale de la porteuse doit être de 1/u0 =4px (resp. 1/v0 =4py) et chaque frange couvre 4 pixels sur la caméra, le nombre total de franges horizontales étant donc de N/4 (resp. M/4).

La figure de franges enregistrée, sur un détecteur matriciel s'écrit :

Ré-écrivons cette expression en faisant apparaître des exponentielles complexes et en tenant compte de la dépendance spatiale :

Posons 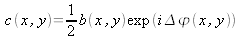et appliquons la transformée de Fourier à l'image enregistrée :

où

et 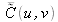est le complexe conjugué de

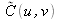
Si les spectres de fréquences spatiales sont étroits par rapport à la fréquence porteuse u0 , on observe trois lobes bien séparés dans le plan de Fourier de l'interférogramme. Les deux lobes symétriques centrés sur +u0 et -u0 contiennent la même information de phase. Il sont simplement complexes conjugués l'un de l'autre. Le filtrage du lobe centré sur la fréquence +u0, par un filtre numérique passe bande bidimensionnel centré en +u0 , permet de ne conserver que l'information de phase qui nous intéresse et conduit donc aussi à un filtrage de la composante continue.

Notons 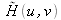la fonction de transfert du filtre. Le filtre est appliqué sur le spectre par multiplication de la transformée de Fourier de l'image avec la fonction de transfert. Nous avons :

Le filtre peut être décrit simplement par une fonction de type « porte à 2 dimensions » de largeurs Δu et Δv :

La transformée de Fourier inverse appliquée à Ẽƒ(u,v) conduit à

Multiplions cƒ(x,y) par 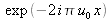on obtient

d'où on déduit la phase optique par une fonction arctangente

Le lecteur remarquera que le filtrage peut également être implanté par convolution dans l'espace de l'interférogramme. En effet, puisque

nous avons aussi dans l'espace direct

où

donnant

Le filtrage numérique pourra être implanté par un filtre linéaire à réponse impulsionnelle finie à 2 dimensions de taille K×K dont la réponse impulsionnelle est :

où L=(K-1)/2.

La résolution spatiale de la méthode est fortement affectée par le choix de la largeur du filtre. Si on note (Rx,Ry) les largeurs au premier zéro de la réponse impulsionnelle du filtre, alors la résolution spatiale est donnée par :

On constate donc qu'on a intérêt à augmenter le plus possible la bande passante du filtre tout en s'assurant qu'il n'y a pas de contributions des autres lobes lors du filtrage.

Le lecteur remarquera que bien que les deux formulations (filtrage spectral et filtrage spatial) soient mathématiquement équivalentes, la mise en oeuvre numérique donnera des résultats différents.

En effet, la synthèse du filtre numérique RIF 2D conduit nécessairement à la troncature du nombre de coefficients puisque la réponse impulsionnelle doit être finie. Cette troncature a pour conséquence l'apparition d'ondulations dans la bande passante et la bande atténuée du filtre. Ainsi, des zones spectrales indésirables peuvent coïncider avec les ondulations, ce qui revient à obtenir un filtrage moins sélectif que la solution qui consiste à couper la zone spectrale directement dans le plan de Fourier.

Cette méthode est très robuste si le rapport signal/bruit dans l'interférogramme biaisé est très bon, dans le cas contraire, bien que le filtrage participe activement à la réduction du bruit, il est possible de rencontrer des problème liés à l'ouverture de franges dans la carte de phase calculée. C'est d'autant plus vrai si la modulation des franges constitue un bruit multiplicatif, comme c'est la cas en interférométrie speckle par exemple. Dans ce cas l'opération de déroulement de phase (« unwrapping ») s'avère délicate.